【斜杠笔记】大学院数学之概率与统计

发表于 2023-02-12 更新于 2023-02-15 分类于斜杠笔记阅读次数： Disqus：本文字数： 1.2k 阅读时长 ≈ 4 分钟

修改记录：

2023.2.13 整理了常见的离散和连续概率变量的概率密度函数

2023.2.15 补充了大学院备考时自己整理的相关考点

待补充：矩母函数和用它来求期望，方差的方法

参考资料：

常用概率分布的矩母函数、特征函数以及期望、方差的推导

https://blog.csdn.net/STcyclone/article/details/84310450

离散型随机变量

1.两点分布（伯努利分布）

$P(X=1)=p,P(X=0)=1-p$

2.均匀分布

$P(X=a_k)=\dfrac{1}{n},k=1,2,\dots,n$

3.二项分布

$P(X=k)=C_n^k p^k(1-p)^{n-k},k=0,1,\dots,n$

4.几何分布

$P(X=k)=(1-p)^{k-1}p,k=1,2,\dots$

5.泊松分布

$P(X=k)=\dfrac{\lambda^k}{k!}e^{-\lambda},k=0,1,2,\dots,\lambda>0$

连续型随机变量

1.均匀分布

$f(x)=\left \{\begin{array}{ll}\dfrac{1}{b-a},&a<x<b\\0,&x\leq a \quad or \quad x\geq b\end{array}\right.$

2.指数分布

$f(x)=\lambda e^{-\lambda x} \quad, \lambda>0$

3.正态分布

\[ f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]

基本概念

確率：偶然起こる現象の現象全てに対する割合のことである。統計：現象を調査することによって数量で把握すること。

事件 $\rightarrow$ 割合 $$计数（加，乘）１）順列２）組み合わせ工具

順列

1）n个球不重复取r个排列 $A_n^r$, 特别当取n个球时，排列方式有$n!$个 2）n个球有放回取r个 $n^r$

3）n个球有同色球，a有$n_1$个，b有$n_2$个 $\dfrac{n!}{n_1!n_2!\dots }$ 4）圆排列 $(n-1)!$

組み合わせ

从n中取r个，组合方式有$C_n^r$ 可重复取时，有$C_{n+r-1}^{n-1}$

事件

$\Omega$全事象

$A_1 \cap A_2$ 積事象　

$A_1 \cup A_2$ 和事象

$A_1 \cap A_2$ 排反

$0\leq P(A) \leq 1$

$P(A_1 A_2)=P(A_1) +P(A_2) - P(A_1A_2) $

加法定理　$P(A_1 \cup A_2 \dots A_k)= P(A_1)+P(A_2)+\dots P(A_k)$

乘法定理 $P(A_1 \cap A_2 \dots \cap A_k) =P(A_1)P(A_2|A_1)P(A_3|A_1\cap A_2)\dots P(A_k|A_1\cap A_2\cap \dots A_{k-1})$

全確率　$P(B)=\sum_{i=1}^n P(A_i) P(B|A_i)$

贝叶斯 $P(A_j|B)=\dfrac{P(B|A_j)P(A_j)}{P(B)}$

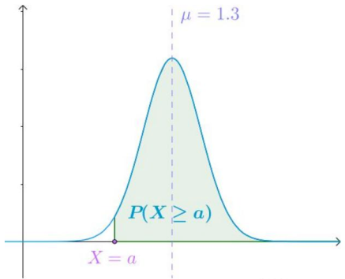
马尔可夫不等式

$P(Xa) $

切比雪夫不等式

$P\{|X-EX|\geq \epsilon \} \leq \dfrac{Var(X)}{\epsilon^2}$ 偏离中心的概率，越远离平均值，概率越低

证明： $P(X\geq a )=\int_0^{+ \infty} f(x)dx \leq \int_a^{+ \infty} f(x)dx$

$E(\dfrac{x}{a})=\int_{- \infty}^a \dfrac{x}{a} f(x)dx +\int_a^{+ \infty} \dfrac{x}{a}f(x)dx$

显然 $\int_{- \infty}^a \dfrac{x}{a}f(x)dx \geq 0$

$\therefore$ $P(x\geq a)\leq \int_a^{+ \infty} \dfrac{x}{a} f(x)dx \leq E(\dfrac{x}{a})$

$\therefore$ $P(x\geq a)\leq E(\dfrac{x}{a})=\dfrac{E(X)}{a}$

将$|x-\mu|$代入 $P(|x-\mu|>a)\leq \dfrac{E(|x-\mu|}{a}$

$\rightarrow P((x-\mu)^2 \leq a^2)\leq \dfrac{E[(x-\mu)^2]}{a^2} =\dfrac{\sigma^2}{a^2}$

令 $k=\dfrac{a}{\sigma}$ 则$k\leq 0, a^2=k^2\sigma^2$

$P(|x-\mu|)\leq k\sigma)\leq \dfrac{1}{k^2}$

大数法则

$x_1,x_2,\dots ,x_n$独立，$E(x_i)=\mu, V(x_i)=\sigma^2$

$\bar{X}=\sum_{i=1} ^n X_i/n, \xi>0$

$\lim_{n\to \infty} P(|\bar{x}-\mu|)\geq \xi)=0$ n次实验抛硬币正面概率趋近于0.5

概率模型

蒲丰投针

$\dfrac{2l}{\pi a}$

取帽子

n个帽子错排号（所有元素都不在原位）客斥原理

1）k=1,错排数 $D_1=0$

2）k=2, $D_2=1$

3）$k\neq n$, n排在第k位， $1\leq k\leq n-1$,那 k在n上，除了n和k还有n-2个数 $D_{n-2}$ k不在n上，将第n位当作新的第k位，含k的n-1个数的第一种错排部等价于 n-1个数的错排

$D_n=(n-1)(D_{n-1}+D_{n-2}$

问题也类似于 N封信，前N-1封可以有N-1或N-2封错装从N-1取1封与第N封错装 $(N-1)D_{n-1}$ 有一封，第N-1封是对的，将其与N封错装 $(N-1)D_{n-2}$

推导过程 $M_1=0, M_2=\frac{1}{2!}$

$D_n=(n-1)(D_{n_1}+D_{n-2})$

记$D_n=n!M_n$

$D_{n-1}=(n-1)!M_{n-1}$, $D_{n-2}=(n-2)!M_{n-2}$

$n!M_n=(n-1)(n-1)!M_{n-1}+(n-1)(n-2)!M_{n-1}$

$=n!M_{n-1}-(n-1)!M_{n-1}+(n-1)!M_{n-2}$ 同时除以(n-1)!

$nM_n=nM_{n-1}-M_{n-1}+M_{n-2}$

$M_n-M_{n-1}=-\frac{1}{n}(M_{n-1}-M_{n-2})$

$=(-\frac{1}{n})(-\frac{1}{n-1})\dots (-\frac{1}{3})(M_2-M_1)$

$=(-1)^{n-2} \cdot \frac{1}{(n-2)!}(\frac{1}{2}-0)$

$=(-1)^n\cdot \frac{1}{n!}$

$\therefore M_n-M_{n-1}=(-1)^n \frac{1}{n!}$

$M_{n-1}-M_{n-2}=(-1)^{n-1} \frac{1}{(n-1)!}$

$\vdots$

$M_2-M_1=(-1)^2 \frac{1}{2!}$

左右累加

$M_n-M_1=M_n=(-1)^2\frac{1}{2!}+(-1)^3\frac{1}{3!}+\dots+(-1)^n\frac{1}{n!}$

$\therefore D_n=n!M_n=n!(\frac{1}{2!}-\frac{1}{3!}+\dots +(-1)^n\frac{1}{n!})$