【斜杠笔记】大学院数学之向量解析
常用向量
1.单位向量
2.基底
向量运算
内积
\(\vec{a}\cdot \vec{b} =x_1x_2+y_1y_2+z_1z_2\)
<a,b>=|a| |b|$ $
几何意义: 向量a在向量b上的投影,再乘以向量b的长度
物理意义:力的分量所作的功
用于判断两个向量的方向及角度:
1)内积>0,夹角小于90度
2)内积=0,垂直
3)内积<0,夹角大于90度
外积
$ =det \[\begin{bmatrix} \vec{i} & \vec{j} & \vec{k} \\x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{bmatrix}\]$
几何意义:
外积的长度\(a\times b =|a||b|\cos \theta\)是两向量围成的平行四边形的面积
物理意义:力矩,如旋转螺丝钉,螺丝钉前进方向垂直于刀口和扭力方向
外积的方向与两向量均垂直,适合求法向量
三重积
1)标量积
\([\vec{a},\vec{b},\vec{c}]=det \begin{bmatrix} x_1 & y_1 &z_1 \\ x_2 & y_2 &z_2 \\x_3 & y_3 &z_3 \end{bmatrix}\)
等于三个列向量组成的行列式的值
几何意义:以三个向量为棱的空间平行六面体的体积
恒等式:
\(a\cdot (b\times c)=b\cdot (c\times a)-c\dot (b\times a )\)
值不变是因为交换了行列式两次,不变号$
2)向量积
\(\vec{a}\times (\vec{b}\times \vec{c} )=b(a\cdot c)-c(a\cdot b)\)
方便记忆小技巧,BAC-CAB,后面有出租车
记忆:三重积一定是两个叉积向量的线性组合
解析几何
基本公式
1)向量微分
\(\dfrac{dA}{dt}=\dfrac{dA_x}{dt}i+\dfrac{dA_y}{dt}j+\dfrac{A_z}{dt}k\)
微分满足分配律和乘积
\(\dfrac{d}{dt}(A+B)=\dfrac{dA}{dt}+\dfrac{dB}{dt}\)
\(\dfrac{d}{dt}(A\cdot B)=\dfrac{dA}{dt}\cdot B+A\cdot \dfrac{dB}{dt}\)
\(\dfrac{d}{dt}(A\times B)=\dfrac{dA}{dt}\times B+A\times \dfrac{dB}{dt}\)
2)向量积分
\(\int Adt =\int A_x dt i+\int A_y dt j+\int A_z dt k\)
直线方程式
点和直线向量
\(x=x_0+k(x_1-x_0)\)
\(y=y_0+k(y_1-y_0)\)
\(z=z_0-k(z_1-z_0)\)
\(\dfrac{x-x_0}{x_1-x_0}=\dfrac{y-y_0}{y_1-y_0}=\dfrac{z-z_0}{z_1-z_0}=t\)
直线向量\(\vec{l}=(x_1,y_1,z_1)\)
平面方程式
平面法向量 \(\vec{n}=(F_x,F_y,F_z)\)
微元3种
1) 线素
沿曲线的向量场和线积分 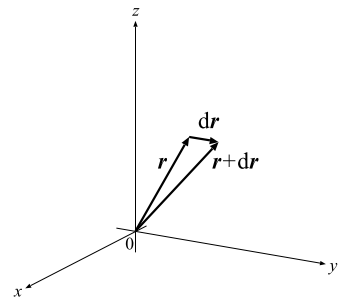
\(s=\int ds =\int |dr| =\int_{t_0}^t |\dfrac{dr}{dr}| dt =\int_{t_0}^t \sqrt{(\dfrac{dx}{dt})^2 +(\dfrac{dy}{dt})^2 +(\dfrac{dz}{dt})^2}\)
线素向量: 空间2点\(\vec{r}\)和\(\vec{r}+d\vec{r}\)之间的微波变化\(d\vec{r}\)
表示曲线上极近的两点\(t_0,t\)之间的一小段弧长
与正常含参曲线的弧长公式一致
单位接线向量:
\(\vec{t}=\dfrac{\vec{dr}}{ds}=\dfrac{\vec{dr}}{dt}\cdot \dfrac{1}{\dfrac{ds}{dt}}\cdot t\cdot t =1\)
ds为曲线微元的长度,当曲线长度无限趋近于某点时,其余斜率等于该点的微分值
2) 面素
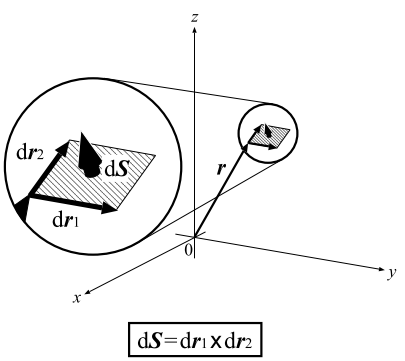
面素:曲面上的向量场的面积分
\(d\vec{S}=\vec{dr_1}\times \vec{dr_2}\)
面素向量的大小用dS表示,二者关系为\(\vec{dS}=\vec{n}dS\)
3)体积要素
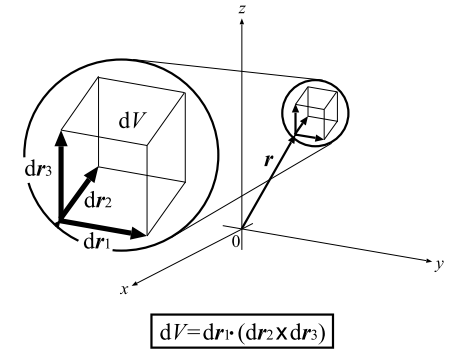
\(dV=\vec{dr_1}\cdot (\vec{dr_2}\times \vec{dr_3})\)
\(\vec{dr_1},\vec{dr_2}, \vec{dr_3}张成的微小平行六面体的体积,所以用混合积表示。\)
线素,面素,体积要素计算
简化运算
闭合曲线积分 - 格林公式
1)针对闭合曲线的积分,可以尝试使用Green公式
若曲线积分$_c P(x,y)dx +Q(x,y)dy $满足以下条件:
1.C是闭合曲线,(D是C围成的密闭领域)
2.C是左向正向(即沿曲线运动,密闭领域在左手边)
3.P(x,y)和Q(x,y)在D内连续可导
则\(\oint_c P(x,y) dx+Q(x,y)dy =\iint_D (\dfrac{\partial Q}{\partial x} -\dfrac{\partial P}{\partial y})\)
闭合曲线积分 - 高斯发散定理
\(\vec{A}是向量场, V是闭曲面S的内部,\vec{n}是S由内向外的单位法向量\)
\(\iint_S \vec{A}\cdot \vec{n} dS =\iiint_V div \vec{A} dV\)
将闭合曲面积分转为三重积分
闭合曲线内的曲面积分 - 斯托克斯定理
\(\vec{A}是向量场,S是闭合曲线C的内部,S是左向正向\)
\(\int_C \vec{A}\cdot \vec{t} dS=\iint_s rot\vec{A} \cdot \vec{n} dS\)
rot 旋度
\(rot \vec{F}=det \begin{bmatrix} \vec{i} & \vec{j} & \vec{k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial }{\partial y} & \dfrac{\partial }{\partial z} \\ F_1 & F_2 & F_3 \end{bmatrix}\)
向量和线性相关
1.n维向量
\(\alpha=[a_1,a_2,\dots, a_n] \quad n个数构成有序数组\)
n维向量
\(\vec{\alpha}^T =[a_1,a_2,\dots,a_n]^T \quad n维列向量\)
加法:
\(\vec{\alpha}+\vec{\beta}=[a_1+b_1,a_2+b_2,\dots,a_n+b_n]\)
数乘:
\(k\vec{\alpha}=[ka_1,ka_2,\dots, ka_n]\)
2.向量线性相关性的概念
线性组合
k个向量
\(\vec{x_1} \sim \vec{x_k}, k个数c_1 \sim c_k 的线性组合\)
线性结合:
$_{i=1}^k c_i $
\(\vec{x_1},\vec{x_2},\dots, \vec{x_k} 的线性结合(1次结合)\)